This article is the third of a series in which I explain what my research is about in (I hope) a simple and straightforward manner. For more details, feel free to check the Research section.

For my first research paper during my PhD, the basic idea was pretty simple. Imagine that, after recording several hours of people being guided around a room, I realize the following: everytime a player stood in front of a door, and someone told them "go straight", they walked through the door. So now I ask: if you are standing in front of a door, and I want you to walk through it, would it be enough for me to say "go straight", like before? My research team and I wanted to give this question an answer, so this is what we did.

We looked at our recorded data. Whenever we saw a player moving somewhere, we took notes about where the player was, where is the player now, and what was the instruction that convinced the player to move from one place to the other. We then created a big dictionary, where each entry reads "to move the player from point A to point B, say this". Quite smart, right?

The most important part about this idea is that we don't need to teach our computer how to understand language - in fact, when our system reads "turn right" in our dictionary, it has no idea about what "turn" or "right" mean. All our system cares about is that saying "turn right", for some strange reason, causes people to look to the right. This makes our system a lot simpler than other systems that try to understand everything.

Now, let's complicate things a bit: let's say I tell you "walk through the door to your left". You turn left, walk through the door, take 7 steps, give a full turn to look at the room, and then you wait for me to say something else. Which of those things you did because I told you, and which ones you did because you felt like it?

Since we didn't really know the answer, we tried two ideas: in the first case, we decided that everything you did was a reaction to our instruction (including the final turn), while in the second one we only considered the first action (turning left), and nothing else. As you can see, neither approach is truly correct: one is too short, and the other one is too long. But in research we like trying simple ideas first, and we decided to give these two a try.

Our results showed that the second approach works better, because if you advance just one step I can guide you to the next, but if you do too many things at once there's a chance you'll get confused and lost. Also, since our system is repeating what other humans said before, players thought the instructions were not too artificial.

Not bad for my first project, right?

This article is the second of a series in which I explain what my research is about in (I hope) a simple and straightforward manner. For more details, feel free to check the Research section.

The GIVE Challenge is a competition started in the University of Saarland, created to collect data about human behavior. Since most of my research is based on that data, it's a good moment to explain what is it about.

We all know GPS by now - whenever we go by car somewhere new, we just type the direction and the GPS guides us. But have you ever thought about how hard it is to give instructions, like your GPS does? For instance, if we are in a roundabout and I say "take the third street to your right", does that mean I have to count all streets, or should I ignore wrong ways? And how much time do you need to react to my directions? These are important question, because they reveal a bit more about how humans act and think.

If we want answers, we need to collect data (reaction times, distance to other cars, misunderstandings, etc), and that data is very difficult to get. For our example, you would have to drive while wearing special glasses, a military GPS, and keep track of all the cars and pedestrians around you. So you might wonder, couldn't we make something simpler, but still useful? My adviser and other researchers asked themselves this exact same question in 2007, and that is how the GIVE Challenge was born.

In GIVE, a person sits in front of a computer, and they play a game. The game is pretty easy - all the person has to do is walk around a virtual house and press some buttons in a certain order. Just like a GPS, they receive instructions telling them where to go and what to do.

In the first variant of the GIVE Challenge, the instructions are given by a person using a computer in a different room. We then record all the information about how the player reacts to the instructions: if the instruction says "turn right", how much does the player turn? Do they just turn, or do they walk too? And how long does it take them? By recording every single movement of the player inside this game, we can answer questions like that.

There's also a second variant: we can write a program that guides the person inside the game, and see how good (or how bad) its instructions are. While a common GPS only cares about streets, our programs have a harder time: humans are not limited to just following streets like cars do, so the instructions are more complex. GIVE is a good way of testing how smart our computers are, and that's why we've been using it for many years now.

We've so far recorded over 340 hours of human movements, divided in 2500 games. Believe it or not this is not too much data, but it's a good start. We have extracted several interesting results from this data, some of which I talk about in future articles.

This article is the first of a series in which I explain what my research is about in (I hope) a simple and straightforward manner. For more details, feel free to check the Research section.

In research, we often want to teach computers how to do a new task, but that is difficult because computers are not too smart, and teaching them even a simple task takes a lot of work. So let's say I want my computer to tell me whether an e-mail is important or not. If I could teach my computer that, then it could show me important e-mails first and save me the trouble of sorting through them daily.

One way of teaching tasks to computers is by doing the job myself, and then make the computer repeat what I did. This is something scientists have been doing for a long time, and today we have a set of steps that every researcher should follow.

The first step is to collect as many e-mails as possible, both important and not. In science, such a big set of e-mails is called a corpus.

Now, just like you wouldn't know what kind of e-mails I consider important, neither does a computer. So the second step is to go through all those e-mails I collected, and mark which ones are important. I'll create two groups, one called "training" and another one called "testing". The first group will contain 4 out of 5 emails, picked at random, while the second group will have the remaining ones.

The third step, unsurprisingly called the training stage, requires the computer to analyze all the e-mails I put in the training group and decide what makes an e-mail important. We would expect our computer to understand, for instance, that since every e-mail containing the word "SALE" was marked as unimportant, then it might be a good idea to mark all e-mails with commercial offers as unimportant. This is by far the hardest step, and there are many ways in which I can influence how well the computer will learn.

The fourth and final step is to give our computer a test, to see whether it learned something useful or not. For this step, called the testing stage, I'll go through each e-mail from the testing group, show the computer the e-mail's text, and ask whether it's important or not. Then I compare the computer's answers with mine, and I'll use that result to decide how good (or how bad) my computer learned the task. If the results are not good enough I can always go back, change how are the e-mails analyzed, and try again. If the results are good, on the other hand, I can trust my program to sort my e-mail from now on.

This is pretty much half my daily work. Collecting enough data (e-mails) is either complicated, expensive, takes a lot of time, or all of that together. And remember I said there are several ways in which a computer might learn? We have to try some of those alternatives too.

Finally, training is usually very slow - in my last project, it took almost a week.

I usually dedicate that time to play Solitaire.

I always associated the word tumbler both with Batman's car in Nolan's movies and with that one website. It turns out that there's a third definition: a tumbler is also a glass, and in particular it is the name for those plastic cups for hot drinks (i.e., coffee) that people carry with them sometimes. They are more or less good for the environment, which is why I ended up with one.

The one I have allows me to change its decoration in a simple way - all I have to do is unscrew the base, remove the current one and replace it with something else. And here is where things become interesting: my tumbler is not shaped like a cylinder, but more like half a cone. Wikipedia calls this figure a frustum, and when you flatten it you end up with a template like this:

So let's say I want to put my own drawing in this format. One could naively make the design, cut it out in the shape of the template, and put it in. If I did this, the entire design would look weird, because the base is smaller than the top, and that messes perspective up in several ways. Luckily, with math we can make it look nice.

Now, before we start, I'm going to give you the summary: if you want to use your own image, make sure that it's size is 21.26cm x 17.43cm (or proportional to that) and then use ImageMagick to run the following command:

convert input.jpg -virtual-pixel White --distort Arc 16.56 output.jpg

So that's out of the way. But where did those numbers come from? Well, let's dust our rulers and take some measurements. I'm going to assume that the template is a slice of a circle with radius (r), like Figure a) shows. Figure b) shows the measures I could obtain accurately. Those are the numbers I got but, of course, if you have a different model your numbers might be different:

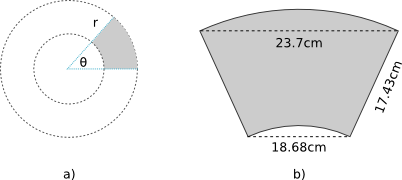
These are easy measures to take, but it doesn't tell me anything about the two main measures I need: the perimeter of the template, and the angle between the non-parallel sides. Why do I need this?

• Measuring the perimeter will allow me to reconstruct the aspect ratio of the original picture. In case you don't know, "aspect ratio" is the relation between the width and the height of an image. Using the wrong one would mean that I'd have to either add black bars to the final design or crop it's sides, and I don't want to do that.
• The angle between the sides will let me deduce at which point both of them would intersect, which I need to calculate (r). Given that we are assuming the template is part of a circle, that would tell me where the center of the circle is.

So let's get down to it. By taking our measures, we can build a trapezoid like the one shown in figure c), along with some names for each side (le=long edge, se=short edge, s=side). Some simple math lets me deduct the lengths for all the relevant sides in figure d), but no angles yet. To get that, we'll need some trigonometry.

Let's cut a triangular slice of our figure. We know the length of two sides (which we use to obtain the third via Pythagoras's theorem), and we also know one of the angles is 90 degrees, or (\frac{\pi}{2}) radians. Using my favorite identity, the Law of sines, we can deduct the angle (\alpha) (see Figure e), which is almost the one we wanted: looking at Figure f), it is clear that (2\alpha) is the angle between the non-parallel sides.

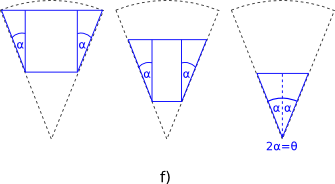
So now let's see if we can get the length of the largest curved side of our tumbler. There are some weird ways of obtaining this value, but I this this is the simpler one: we know already that (2 \pi r) gives us the full circumference of a circle. But we don't want the full circumference, just a small piece of it - more precisely, a piece with an angle (\theta = 2\alpha).

Now that you got the basic idea, this is what I'm doing next:

• Make a triangle with angle (\alpha) similar to the previous one, but one that goes all the way to the center of the circle. Note that the sides are now larger, but the angle remains unchanged.
• For this new triangle, its length (s) equals the length (r) (which we don't know yet) and the length of its shorter side is (\frac{le}{2}).
• Having two angles and one side, I'll use my favorite identity again to calculate the length of the unknown side (s) (which equals (r)).
• The end result is that (r = 82.29cm).

Cool! Now that we have (r), we can obtain the circumference of our circle. If we obtain the circumference only for an angle (\theta), we get the length of the long curved side, which is 23.78cm, and the length of the short side, which is the same calculation but subtracting (s) from (r). That tells us the shorter curved side is 18.75cm, and now I have all the measures I need to properly draw and deform my picture. Imagine for a second that our original picture is made of rubber, and we deform it until it looks like the shape of our tumbler's label. Then the top of our picture would be stretched, while the bottom would be compressed. So if we want to know how wide was our original picture, we want to check right in the middle of the picture, which is the only part that would not be deformed. That length is 21.26cm (i.e., the average between both sides), and now that we know our original picture was 21.26cm x 17.43cm, we can divide and get a frankly terrible ratio of 1.219, which is the aspect ratio we need for our pictures to fit just right.

So that's that. We now know how to properly set up our original design, and we have all the numbers to deform it properly, but how do we actually deform it? Well, as I'm a GNU-Linux guy, I'm going to go ahead and suggest you use ImageMagick. More specifically, the command I mentioned at the beginning of the article - although now you know why your picture needs to be a certain size and where the value of (\theta) comes from.

And just like that, we have our picture ready to be printed. Make sure that your picture is printed exactly 23.7cm wide, pick some scissors, and you now have a perspective corrected, formally verified new tumbler skin.

A random collection of things I saw on the internet:

• A great strip from the Doonesbury comic strip.