Benchmarking Python loops
April 21: see the "Update" section at the end for a couple extra details.
A very common operation when programming is iterating over elements with a nested loop: iterate over all entities in a collection and, for each element, perform a second iteration. A simple example in a bank setting would be a job where, for each customer in our database, we want to sum the balance of each individual operation that the user performed. In pseudocode, it could be understood as:
for each customer in database:
customer_balance=0
for each operation in that user:
customer_balance = customer_balance + operation.value
# At this point, we have the balance for this one customer
Of all the things that Python does well, this is the one at which Python makes it very easy for users to do it wrong. But for new users, it might not be entirely clear why. In this article we'll explore what the right way is and why, by following a simple experiment: we create an n-by-n list of random values, measure how long it takes to sum all elements three times, and display the average time in seconds to see which algorithm is the fastest.
values = [[random.random() for _ in range(n)] for _ in range(n)]
We will try several algorithms for the sum, and see how they improve over each other. Method 1 is the naive one, in which we implement a nested for-loop using variables as indices:
for i in range(n):
for j in range(n):
acum += values[i][j]
This method takes 42.9 seconds for n=20000, which is very bad.
The main problem here is the use of the i and j variables. Python's dynamic
types and duck typing means that,
at every iteration, the interpreter needs to check...
- ... what the type of
iis - ... what the type of
jis - ... whether
valuesis a list - ... whether
values[i][j]is a valid list entry, and what its type is - ... what the type of
acumis - ... whether
values[i][j]andacumcan be summed and, if so, how - summing two strings is different from summing two integers, which is also different from summing an integer and a float.
All of these checks make Python easy to use, but it also makes it slow. If we want to get a reasonable performance, we need to get rid of as many variables as possible.
Method 2 still uses a nested loop, but now we got rid of the indices and replaced them with list comprehension
for row in values:
for cell in row:
acum += cell
This method takes 17.2 seconds, which is a lot better but still kind of bad.
We have reduced the number of type checks (from 4 to 3), we removed two
unnecesary objects (by getting rid of range), and acum += cell only needs
one type check. Given that we still need checking for cell and row,
we should consider getting rid of them too.
Method 3 and Method 4 are alternatives to using even less variables:
# Method 3
for i in range(n):
acum += sum(values[i])
# Method 4
for row in values:
acum += sum(row)
Method 3 takes 1.31 seconds, and Method 4 pushes it even further with
1.27 seconds. Once again, removing the i variable speed things up,
but it's the "sum" function where the performance gain comes from.
Method 5 replaces the first loop entirely with the map function.
acum = sum(map(lambda x: sum(x), values))
This doesn't really do much, but it's still good: at 1.30 seconds, it is faster than Method 3 (although barely). We also don't have much code left to optimize, which means it's time for the big guns.
NumPy is a Python library for scientific applications. NumPy has a stronger type check (goodbye duck typing!), which makes it not as easy to use as "regular" Python. In exchange, you get to extract a lot of performance out of your hardware.
NumPy is not magic, though. Method 6 replaces the nested list values
defined above with a NumPy array, but uses it in a dumb way.
array_values = np.random.rand(n,n)
for i in range(n):
for j in range(n):
acum += array_values[i][j]
This method takes an astonishing 108 seconds, making it by far the worst performing of all. But fear not! If we make it just slightly smarter, the results will definitely pay off. Take a look at Method 7, which looks a lot like Method 5:
acum = sum(sum(array_values))
This method takes 0.29 seconds, comfortably taking the first place. And even then, Method 8 can do better with even less code:
acum = numpy.sum(array_values)
This brings the code down to 0.16 seconds, which is as good as it gets without any esoteric optimizations.
As a baseline, I've also measured the same code in single-threaded C code. Method 9 implements the naive method:
float **values;
// Initialization of 'values' skipped
for(i=0; i<n; i++)
{
for(j=0; j<n; j++)
{
acum += values[i][j];
}
}
Method 9 takes 0.9 seconds, which the compiler can optimize to 0.4 seconds
if we compile with the -O3 flag (listed in the results as Method 9b).
All of these results are listed in the following table, along with all the
values of n I've tried.
While results can jump a bit depending on circumstances (memory usage,
initialization, etc), I'd say they look fairly stable.
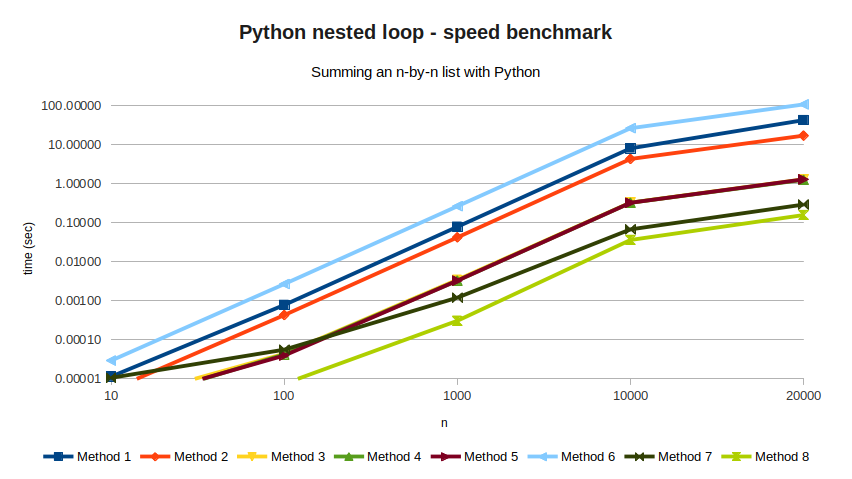
| N=10 | N=100 | N=1000 | N=10000 | N=20000 | |
|---|---|---|---|---|---|
| Method 1 | 0.00001 | 0.00078 | 0.07922 | 8.12818 | 42.96835 |
| Method 2 | 0.00001 | 0.00043 | 0.04230 | 4.34343 | 17.18522 |
| Method 3 | 0.00000 | 0.00004 | 0.00347 | 0.33048 | 1.30787 |
| Method 4 | 0.00000 | 0.00004 | 0.00329 | 0.32733 | 1.27049 |
| Method 5 | 0.00000 | 0.00004 | 0.00329 | 0.32677 | 1.30128 |
| Method 6 | 0.00003 | 0.00269 | 0.26630 | 26.61225 | 108.61357 |
| Method 7 | 0.00001 | 0.00006 | 0.00121 | 0.06803 | 0.29462 |
| Method 8 | 0.00001 | 0.00001 | 0.00031 | 0.03640 | 0.15836 |
| Method 9 | 0.00000 | 0.00011 | 0.00273 | 0.22410 | 0.89991 |
| Method 9b | 0.00000 | 0.00006 | 0.00169 | 0.09978 | 0.40069 |
Final thoughts
I honestly don't know how to convey to Python beginners what the right way to do loops in Python is. With Python being beginner-friendly and Method 1 being the most natural way to write a loop, running into this problem is not a matter of if, but when. And any discussion of Python that includes terms like "type inference" is likely to go poorly with the crowd that needs it the most. I've also seen advice of the type "you have to do it like this because I say so and I'm right" which is technically correct but still unconvincing.
Until I figure that out, I hope at least this short article will be useful for intermediate programmers like me who stare at their blank screen and wonder "two minutes to sum a simple array? There has to be a better way!".
Further reading
If you're a seasoned programmer, Why Python is slow answers the points presented here with a deep dive into what's going on under the hood.
April 21 Update
A couple good points brought up by my friend Baco:
- The results between Methods 3, 4, and 5 are not really statistically significant. I've measured them against each other and the best I got was a marginal statistical difference between Methods 3 and 5, also known as "not worth it".
- Given that they are effectively the same, you should probably go for Method 4, which is the easiest one to read out of those three.
- If you really want to benchmark Python, you should try something more challenging than a simple sum. Matrix multiplication alone will give you different times depending on whether you use liblapack3 or libopenblas as a dependency. Feel free to give it a try!
